Here is the math I promised on why nonlinear weighting (exponent less than 1) works quite well while linear weighting does not
Current state of affairs:
Let R0 be node rewards under current implementation. For the sake of argument lets assume an average value that happens to be around 40 POKT in today’s environment
Let C be the average daily operating cost of a node priced in POKT; in today’s environment this is very close to R0; i.e., around 40 POKT. Since C is more or less a fixed fiat price, the main sensitivity of C is to the price of POKT. When POKT is $1 C is approx. 5; if POKT were to drop to 5 cents, C may be closer to 100
Let k be the number of nodes a node runner (pool/DAO/whale etc) runs. Let’s assume k large compared to 5 (so that he can consolidate to larger nodes if that were made possible) (i.e., k=100 would be someone with 1.5M POKT running 100 nodes)
Let P be the total payout to the node runner:
P = k*(R0 – C)
which clearly is untenable when C>=R0 as in today’s environment
State of affairs if PIP-22 gets passed as-is (stated in simplified terms):
R = R0 * A * B *min(n,m)
where A is a DOA-controlled parameter (currently suggested to be set to 1/5 or slightly larger),
B is an unknown network multiplier that depends on how effective PIP-22 is in reducing node count,
n is the quantized multiple of 15k POKT that an operator wishes to stake to a node,
and m is a DAO-controlled parameter (currently suggested to be set to 5)
total payout to node runner becomes:
P = k/n * (R-C) = k/n * (R0 * A * B * min (n,m) – C)
The continuation of the math will be easier to show if we take the cap out of the equation and just remember that the cap exists and apply it in the end. Thus, for n<=m:
P = k/n * (R0 * A * B * n – C)
= k * R0 * A * B - k * C/n
A node runner is motivated to maximize their payout and will adjust n accordingly. To find the max payout as a function of n, take the first derivative of P(n) and find where this crosses 0 (if at all)
dP/dn = k*C / (n^2) == 0 which implies n = infinity (but capped of course at m)
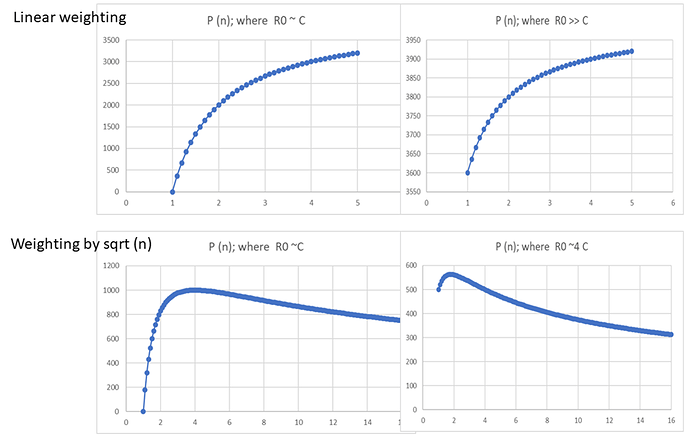
Or to show this visually instead of mathematically, this is payout as a function of n for challenging times like now where node reduction is needed compared to times where POKT is flying high and node growth is needed
(See graphic at the end)
Meaning that no matter the attempt by the DAO to tweak parameters, no matter the network effect caused by consolidation and no matter the economic environment or the need to add nodes, node runners will never be able to be incentive to run a node at anything less than the max POKT allowed. Great for times like now where node reductions is warranted – horrible in the long term when node growth is needed
Now compare this to what happens if we weight by the sqrt of n rather than linear with n (ignoring for the moment the possible setting of a cap).
R = R0 * A * B *sqrt(n)
where A,B and n have the same meaning as in the above discussion
P = k/n * (R – C)
= k/n * (R0 * A * B * sqrt(n) – C)
= k * R0 * A * B/sqrt(n) – k * C/n
Again, a node runner is motivated to maximize their payout and will adjust n accordingly. To find the max payout as a function of n, take the first derivative of P(n) and find where this crosses 0 (if at all)
dP/dn = k/(n^2) (C – R0ABsqrt(n)/2) ==0 n for max payout is at n = 4 (C/(R0A*B)^2
For given averages for R0, C and B, the DAO can now easily skew node-runner behavior toward running max-sized nodes, min-sized nodes or anything in between. 0.25 is a suggested initial value for A. This should cause most operators who can, to consolidate toward n=4 (60k POKT staked per node)
The system is self-correcting with respect to the network affects of consolidation (unknown variable B). At the start when few nodes are consolidated node runners are incentivized to consolidate. IF node runners consolidate too strongly (say they start staking 200k POKT per node) B shoots past target and the yield curve adjust to strongly incentivize destaking back down to about 60k POKT per node) and open back up more nodes
This also exhibits correct behavior with respect to economic conditions. Suppose POKT price drops to $0.05 to $0.1, (C>R0) then this incentivizes node runners to consolidate to even greater levels (max payout t around n=7 ~105k POKT staked per node). At a POKT price of $.4 (C<R0) sweet spot drops from n=4 to between 2 and 3). If POKT price jumps up to $2 (C<<R0) because relays are shooting through the roof, sweet spot drops to the n=1 to 2 range.)
Note this example only shows the effect of weighting by sqrt(n). It is better probably to weight by n^p where p is a DAO controlled parameter between 0 and 1 I have to model further, but I think p closer to 2/3 may give more desireable results (in terms of curve steepness etc) than p=1/2, but I will not know until I have a chance to model it.